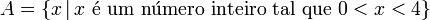Conjunto

Origem: Wikipédia, a enciclopédia livre.

(Redirecionado de Conjuntos)

Ir para: navegação, pesquisa

Este artigo ou secção cita fontes fiáveis e independentes, mas elas não cobrem todo o texto.
Por favor, melhore este artigo providenciando mais fontes fiáveis e independentes, inserindo-as em notas de rodapé ou no corpo do texto, nos locais indicados.
Encontre fontes: Google — notícias, livros, acadêmico — Scirus. Veja como referenciar e citar as fontes.

Na matemática, um conjunto é uma coleção de elementos^[1]. A relação básica entre um objeto e o conjunto é a relação de pertinência: quando um objeto x é um dos elementos que compõem o conjunto A, dizemos que x pertence a A ^[2].
Nos conjuntos, a ordem e a quantidade de vezes que os elementos estão listados na coleção não é relevante. Em contraste, uma coleção de elementos na qual a multiplicidade, mas não a ordem, é relevante, é chamada multiconjunto. Dizemos que dois conjuntos são iguais se e somente se cada elemento de um é também elemento do outro.

Índice

[esconder]

1 Importância
2 Notação matemática
3 Conceitos essenciais
- 3.1 Subconjuntos próprios e impróprios
- 3.2 Conjunto vazio
- 3.3 Cardinalidade
- 3.4 Conjunto potência ou de partes
- 3.5 Produto cartesiano
4 Operações com conjuntos
5 Conjuntos compostos por números
6 Ver também
7 Referências

[editar] Importância

Um conjunto é considerado um dos conceitos mais básicos da matemática, sendo o elemento principal da teoria dos conjuntos.

[editar] Notação matemática

É possível descrever o mesmo conjunto de três maneiras diferentes, por meio de uma:

lista os seus elementos (ideal para conjuntos pequenos e finitos);
definição de uma propriedade de seus elementos (o que, se for feito de forma descuidada, pode gerar problemas, tais como o paradoxo de Russell);
representação gráfica.

A notação padrão em Matemática lista os elementos separados por vírgulas e delimitados por chaves (o uso de "parênteses" ou "colchetes" é incomum e, em determinados contextos, considerado incorreto). Um conjunto A, por exemplo, poderia ser representado como:

$A=\left\{1, 2, 3 \right\}\,\!$

Como a ordem não importa em conjuntos, isso é equivalente a escrever, por exemplo:

$A=\left\{1, 2, 2, 1, 3, 2\right\}\,\!$

Um conjunto ABCDEFGHIJ também fica definido (ou determinado, ou caracterizado) quando se dá uma regra que permita decidir se um objeto arbitrário pertence ou não a A. Por exemplo, a frase "B é o conjunto dos triângulos retângulos" define perfeitamente o conjunto B, já que permite decidir se um objeto qualquer é ou não elemento de B^[3]. O mesmo conjunto A do parágrafo anterior poderia ser representado por uma regra:

$A= \left\{ x\,|\,x \mbox{ é um número inteiro tal que } 0 < x < 4 \right\}$

ou ainda:

$A= \left\{ x\,:\,x \mbox{ é um número natural tal que } 1 \le x \le 3 \right\}$

Note que as propriedades ou descrições de um conjunto são representadas dentro das {}, após os elementos e separadas destes por : ou por |.
Também é possível representar graficamente os conjuntos. O Diagrama de Venn-Euler é a representação gráfica dos conjuntos, através de entidades geométricas.

[editar] Conceitos essenciais

Conjunto: representa uma coleção de objetos, geralmente representado por letras maiúsculas;
Elemento: qualquer um dos componentes de um conjunto, geralmente representado por letras minúsculas;
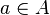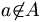Pertinência: é a característica associada a um elemento que faz parte de um conjunto. Se $a$ é um elemento de $A$ , podemos dizer que o elemento $a$ pertence ao conjunto $A$ e podemos escrever $a \in A$ . Se $a$ não é um elemento de $A$ , nós podemos dizer que o elemento $a$ não pertence ao conjunto $A$ e podemos escrever $a \not\in A$ .

[editar] Subconjuntos próprios e impróprios

Ver artigo principal: Subconjunto

Se $A \,\!$ e $B \,\!$ são conjuntos e todo o elemento $x \,\!$ pertencente a $A \,\!$ também pertence a $B \,\!$ , então o conjunto $A \,\!$ subconjunto do conjunto $B \,\!$ , denotado por $A \subseteq B$ . Note que esta definição inclui o caso em que $A$ e $B$ possuem os mesmos elementos, isto é, são o mesmo conjunto ( $A = B$ ). 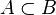Se $A \subseteq B$ e ao menos um elemento pertencente a $B \,\!$ não pertence a $A \,\!$ , então $A \,\!$ é chamado de subconjunto próprio de $B \,\!$ , denotado por $A \subset B$ . Todo conjunto é subconjunto dele mesmo, entretanto não se enquadra na definição de subconjunto próprio, e é chamado de subconjunto impróprio. é dito um

$A \subseteq B$

[editar] Conjunto vazio

Ver artigo principal: Conjunto vazio

Todo conjunto também possui como subconjunto o conjunto vazio representado por { } ou $\emptyset$ .
Podemos mostrar isto supondo que se o conjunto vazio não pertence ao conjunto em questão, então o conjunto vazio deve possuir um elemento ao menos que não pertença a este conjunto. Como o conjunto vazio não possui elementos, isto não é possível. Como todos os conjuntos vazios são iguais uns aos outros, é permissível falar de um único conjunto sem elementos.

[editar] Cardinalidade

Ver artigo principal: Cardinalidade

Se um conjunto tem n elementos, onde n é um número natural (possivelmente 0), então diz-se que o conjunto é um conjunto finito com uma cardinalidade de n ou número cardinal n.
Mesmo se o conjunto não possui um número finito de elementos, pode-se definir a cardinalidade, graças ao trabalho desenvolvido pelo matemático Georg Cantor. Neste caso, a cardinalidade poderá ser $\aleph_0$ (aleph-0), 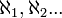$\aleph_1, \aleph_2 ...$ .
Nos dois casos a cardinalidade de um conjunto $A$ é denotada por $| A |$ . Se para dois conjuntos A e B é possível fazer uma relação um-a-um entre seus elementos, então $| A | = | B |$ .

[editar] Conjunto potência ou de partes

Ver artigo principal: Conjunto de partes

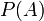O conjunto de todos os subconjuntos de um conjunto dado $A$ é chamado de conjunto potência (ou conjunto das partes) de $A$ , denotado por $P(A)\,\!$ . O conjunto potência é uma álgebra booleana sobre as operações de união e interseção.
Sendo o conjunto dado A finito, com n elementos, prova-se que o número de subconjuntos ou o número de elementos do conjunto potência ou conjunto das partes de A é $2 n$ , ou seja, a cardinalidade do conjunto das partes de A é igual a $2 n$ . Como existe uma bijecção entre o conjunto das partes de A e o conjunto ${0,1} A$ , é usual representar-se P(A) por $2^A\,\!$ .
O Teorema de Cantor estabelece que $|A| < |P(A)|\,\!$ .

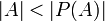[editar] Produto cartesiano

Ver artigo principal: Produto cartesiano

O produto cartesiano de dois conjuntos A e B é o conjunto de pares ordenados:

$A \times B= \{(a,b) : a \in A \and b \in B\}$

A soma ou união disjunta de dois conjuntos A e B é o conjunto

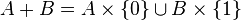$A + B = A \times \{0\} \cup B \times \{1\}$ .

[editar] Operações com conjuntos

De maneira semelhante ao que ocorre com os números, também existem operações matemáticas com conjuntos. Nos exemplos são utilizados diagramas de Venn para ilustrar.

Operação	Operador	Definição	Exemplo
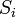União	$\cup$	A união (ou reunião) de dois conjuntos $A \,\!$ e $B \,\!$ é o conjunto $A \cup B$ composto dos elementos que pertencem ao menos a um dos conjuntos $A \,\!$ ou $B \,\!$ . A união de N conjuntos $S = S_1 \cup S_2 \cup S_3 \cdots \cup S_N = \cup_{i=1}^N S_i$ $S_i \,\!$ . A união entre dois conjuntos pode ser definida formalmente por $A \cup B=\{\forall x\|x\in A \or x\in B\}$ é o conjunto formado pelos os elementos que pertencem ao menos a um dos conjuntos	$A \cup B$
Interseção	$\cap$	A interseção de dois conjuntos $A \,\!$ e $B \,\!$ é o conjunto $A \cap B$ composto dos elementos que pertencem simultaneamente aos dois conjuntos $A \,\!$ $B \,\!$ . e	$A \cap B$
Diferença	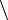$\setminus$ ou $-$	A diferença 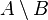$A \setminus B$ ( ou $A\,\!$ $-$ $B\,\!$ ) entre dois conjuntos $A \,\!$ e $B \,\!$ é o conjunto dos elementos que pertencem a $A \,\!$ e que não pertencem a $B \,\!$ .	$A \setminus B$

[editar] Conjuntos compostos por números

Nota: Nesta seção, a, b e c são números naturais, enquanto r, s, t e u são números reais.

Números naturais são usados para contar. O símbolo $\mathbb{N}$ usualmente representa este conjunto. Na literatura matemática, é possível encontrar textos que incluem o zero como número natural e textos que não incluem.
Números primos aparecem na fatoração de números inteiros. O símbolo $\mathbb{P}$ usualmente representa este conjunto.
Números inteiros aparecem como soluções de equações como x + a = b. O símbolo $\mathbb{Z}$ usualmente representa este conjunto (do termo alemão Zahlen que significa números).
Números racionais aparecem como soluções de equações como a + bx = c. O símbolo $\mathbb{Q}$ usualmente representa este conjunto (da palavra quociente).
Números irracionais são números reais que não são números racionais. O símbolo 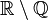$\mathbb{R}\setminus\mathbb{Q}$ usualmente representa este conjunto.
Números algébricos aparecem como soluções de equações polinomiais (com coeficientes inteiros) e envolvem raízes e alguns outros números irracionais. O símbolo 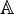$\mathbb{A}$ ou $\bar{\mathbb{Q}}$ usualmente representa este conjunto.
Números transcendentais são números reais que não são números algébricos. O símbolo $\mathbb{R}\setminus\mathbb{A}$ usualmente representa este conjunto.
Números reais incluem os números algébricos e os números transcendentais. O símbolo $\mathbb{R}$ usualmente representa este conjunto. (O estudo destes conjuntos é tão importante que recebe até nome específico: análise real.)
Números imaginários aparecem como soluções de equações como x ² + r = 0 onde r > 0. O símbolo $\mathbb{I}$ ou $i \mathbb{R}$ usualmente representa este conjunto.
Números complexos é a soma dos números reais e dos imaginários: $r + s i$ . O símbolo $\mathbb{C}$ usualmente representa este conjunto.
Números quaterniões é a soma de números reais e de três números imaginários de unidades distintas: $r + s i + t j + u k$ . O símbolo $\mathbb{H}$ usualmente representa este conjunto.
Números octoniões é a soma de números reais e de sete números imaginários de unidades distintas. O símbolo 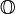$\mathbb{O}$ usualmente representa este conjunto.
Números complexos hiperbólicos é a soma de números reais com uma unidade que satisfaz $\jmath^2 = 1$ e $\jmath \neq \pm 1$ . Os números complexos hiperbólicos são da forma $r + s\jmath$ . Aqui tanto r quanto s podem ser iguais a zero. O símbolo $\mathbb{R}^{1,1}$ usualmente representa este conjunto.
Números p-ádicos são uma extensão dos números inteiros, onde p é um número primo. Os símbolos 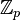$\mathbb{Z}_p$ usualmente representam estes conjuntos. (não confundir com inteiros módulo p)
Números ordinais aparecem em Teoria dos Conjuntos. Não existe o conjunto dos números ordinais.
Números cardinais aparecem em Teoria dos Conjuntos. Um número cardinal é um número ordinal que não é equipotente a nenhum ordinal menor do que ele. Não existe o conjunto dos números cardinais.