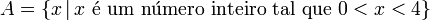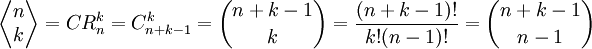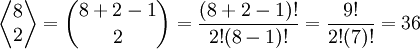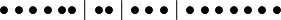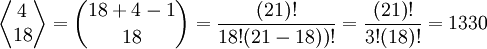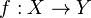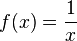Conjunto
Origem: Wikipédia, a enciclopédia livre.
(Redirecionado de Conjuntos)
Na matemática, um conjunto é uma coleção de elementos[1]. A relação básica entre um objeto e o conjunto é a relação de pertinência: quando um objeto x é um dos elementos que compõem o conjunto A, dizemos que x pertence a A [2].Nos conjuntos, a ordem e a quantidade de vezes que os elementos estão listados na coleção não é relevante. Em contraste, uma coleção de elementos na qual a multiplicidade, mas não a ordem, é relevante, é chamada multiconjunto. Dizemos que dois conjuntos são iguais se e somente se cada elemento de um é também elemento do outro.
Índice[esconder] |
[editar] Importância
Um conjunto é considerado um dos conceitos mais básicos da matemática, sendo o elemento principal da teoria dos conjuntos.[editar] Notação matemática
É possível descrever o mesmo conjunto de três maneiras diferentes, por meio de uma:- lista os seus elementos (ideal para conjuntos pequenos e finitos);
- definição de uma propriedade de seus elementos (o que, se for feito de forma descuidada, pode gerar problemas, tais como o paradoxo de Russell);
- representação gráfica.
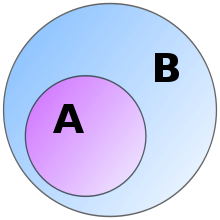
Também é possível representar graficamente os conjuntos. O Diagrama de Venn-Euler é a representação gráfica dos conjuntos, através de entidades geométricas.
[editar] Conceitos essenciais
- Conjunto: representa uma coleção de objetos, geralmente representado por letras maiúsculas;
- Elemento: qualquer um dos componentes de um conjunto, geralmente representado por letras minúsculas;
- Pertinência: é a característica associada a um elemento que faz parte de um conjunto. Se a é um elemento de A, podemos dizer que o elemento a pertence ao conjunto A e podemos escrever
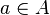 . Se a não é um elemento de A, nós podemos dizer que o elemento a não pertence ao conjunto A e podemos escrever
. Se a não é um elemento de A, nós podemos dizer que o elemento a não pertence ao conjunto A e podemos escrever 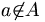 .
.
[editar] Subconjuntos próprios e impróprios
 e
e  são conjuntos e todo o elemento
são conjuntos e todo o elemento 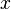 pertencente a
pertencente a  também pertence a
também pertence a  , então o conjunto
, então o conjunto  é dito um subconjunto do conjunto
é dito um subconjunto do conjunto  , denotado por
, denotado por 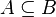 . Note que esta definição inclui o caso em que A e B possuem os mesmos elementos, isto é, são o mesmo conjunto (A = B). Se
. Note que esta definição inclui o caso em que A e B possuem os mesmos elementos, isto é, são o mesmo conjunto (A = B). Se 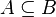 e ao menos um elemento pertencente a
e ao menos um elemento pertencente a  não pertence a
não pertence a  , então
, então  é chamado de subconjunto próprio de
é chamado de subconjunto próprio de  , denotado por
, denotado por 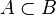 . Todo conjunto é subconjunto dele mesmo, entretanto não se enquadra na definição de subconjunto próprio, e é chamado de subconjunto impróprio.
. Todo conjunto é subconjunto dele mesmo, entretanto não se enquadra na definição de subconjunto próprio, e é chamado de subconjunto impróprio.[editar] Conjunto vazio
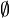 .
.Podemos mostrar isto supondo que se o conjunto vazio não pertence ao conjunto em questão, então o conjunto vazio deve possuir um elemento ao menos que não pertença a este conjunto. Como o conjunto vazio não possui elementos, isto não é possível. Como todos os conjuntos vazios são iguais uns aos outros, é permissível falar de um único conjunto sem elementos.
[editar] Cardinalidade
Mesmo se o conjunto não possui um número finito de elementos, pode-se definir a cardinalidade, graças ao trabalho desenvolvido pelo matemático Georg Cantor. Neste caso, a cardinalidade poderá ser
 (aleph-0),
(aleph-0), 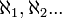 .
.Nos dois casos a cardinalidade de um conjunto A é denotada por | A | . Se para dois conjuntos A e B é possível fazer uma relação um-a-um entre seus elementos, então | A | = | B | .
[editar] Conjunto potência ou de partes
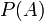 . O conjunto potência é uma álgebra booleana sobre as operações de união e interseção.
. O conjunto potência é uma álgebra booleana sobre as operações de união e interseção.Sendo o conjunto dado A finito, com n elementos, prova-se que o número de subconjuntos ou o número de elementos do conjunto potência ou conjunto das partes de A é 2n, ou seja, a cardinalidade do conjunto das partes de A é igual a 2n. Como existe uma bijecção entre o conjunto das partes de A e o conjunto {0,1}A, é usual representar-se P(A) por
 .
.O Teorema de Cantor estabelece que
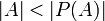 .
.[editar] Produto cartesiano
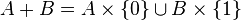 .
.
[editar] Operações com conjuntos
De maneira semelhante ao que ocorre com os números, também existem operações matemáticas com conjuntos. Nos exemplos são utilizados diagramas de Venn para ilustrar.| Operação | Operador | Definição | Exemplo | |
|---|---|---|---|---|
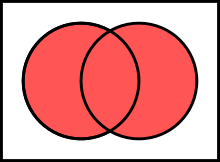
| União |  | A união (ou reunião) de dois conjuntos  e e  é o conjunto é o conjunto  composto dos elementos que pertencem ao menos a um dos conjuntos composto dos elementos que pertencem ao menos a um dos conjuntos  ou ou  . A união de N conjuntos . A união de N conjuntos  é o conjunto formado pelos os elementos que pertencem ao menos a um dos conjuntos é o conjunto formado pelos os elementos que pertencem ao menos a um dos conjuntos 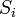 . A união entre dois conjuntos pode ser definida formalmente por . A união entre dois conjuntos pode ser definida formalmente por  | ||
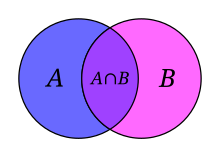
| Interseção |  | A interseção de dois conjuntos  e e  é o conjunto é o conjunto  composto dos elementos que pertencem simultaneamente aos dois conjuntos composto dos elementos que pertencem simultaneamente aos dois conjuntos  e e  . . | ||
| Diferença | 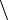 ou − ou − | A diferença  ( ou ( ou  − −  ) entre dois conjuntos ) entre dois conjuntos  e e  é o conjunto dos elementos que pertencem a é o conjunto dos elementos que pertencem a  e que não pertencem a e que não pertencem a  . . |
[editar] Conjuntos compostos por números
Nota: Nesta seção, a, b e c são números naturais, enquanto r, s, t e u são números reais.- Números naturais são usados para contar. O símbolo
 usualmente representa este conjunto. Na literatura matemática, é possível encontrar textos que incluem o zero como número natural e textos que não incluem.
usualmente representa este conjunto. Na literatura matemática, é possível encontrar textos que incluem o zero como número natural e textos que não incluem. - Números primos aparecem na fatoração de números inteiros. O símbolo
 usualmente representa este conjunto.
usualmente representa este conjunto. - Números inteiros aparecem como soluções de equações como x + a = b. O símbolo
 usualmente representa este conjunto (do termo alemão Zahlen que significa números).
usualmente representa este conjunto (do termo alemão Zahlen que significa números). - Números racionais aparecem como soluções de equações como a + bx = c. O símbolo
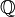 usualmente representa este conjunto (da palavra quociente).
usualmente representa este conjunto (da palavra quociente). - Números irracionais são números reais que não são números racionais. O símbolo
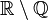 usualmente representa este conjunto.
usualmente representa este conjunto. - Números algébricos aparecem como soluções de equações polinomiais (com coeficientes inteiros) e envolvem raízes e alguns outros números irracionais. O símbolo
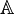 ou
ou  usualmente representa este conjunto.
usualmente representa este conjunto. - Números transcendentais são números reais que não são números algébricos. O símbolo
 usualmente representa este conjunto.
usualmente representa este conjunto. - Números reais incluem os números algébricos e os números transcendentais. O símbolo
 usualmente representa este conjunto. (O estudo destes conjuntos é tão importante que recebe até nome específico: análise real.)
usualmente representa este conjunto. (O estudo destes conjuntos é tão importante que recebe até nome específico: análise real.) - Números imaginários aparecem como soluções de equações como x ² + r = 0 onde r > 0. O símbolo
 ou
ou  usualmente representa este conjunto.
usualmente representa este conjunto. - Números complexos é a soma dos números reais e dos imaginários: r + si. O símbolo
 usualmente representa este conjunto.
usualmente representa este conjunto. - Números quaterniões é a soma de números reais e de três números imaginários de unidades distintas: r + si + tj + uk. O símbolo
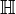 usualmente representa este conjunto.
usualmente representa este conjunto. - Números octoniões é a soma de números reais e de sete números imaginários de unidades distintas. O símbolo
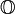 usualmente representa este conjunto.
usualmente representa este conjunto. - Números complexos hiperbólicos é a soma de números reais com uma unidade que satisfaz
 e
e  . Os números complexos hiperbólicos são da forma
. Os números complexos hiperbólicos são da forma  . Aqui tanto r quanto s podem ser iguais a zero. O símbolo
. Aqui tanto r quanto s podem ser iguais a zero. O símbolo  usualmente representa este conjunto.
usualmente representa este conjunto. - Números p-ádicos são uma extensão dos números inteiros, onde p é um número primo. Os símbolos
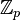 usualmente representam estes conjuntos. (não confundir com inteiros módulo p)
usualmente representam estes conjuntos. (não confundir com inteiros módulo p) - Números ordinais aparecem em Teoria dos Conjuntos. Não existe o conjunto dos números ordinais.
Teoria dos conjuntos
Origem: Wikipédia, a enciclopédia livre.
Teoria dos conjuntos é o ramo da matemática que estuda conjuntos, que são coleções de objetos. Embora qualquer tipo de objeto possa ser reunido em um conjunto, a teoria dos conjuntos é aplicada na maioria das vezes a objetos que são relevantes para a matemática. A linguagem da teoria dos conjuntos pode ser usada nas definições de quase todos os objetos matemáticos.O estudo moderno da teoria dos conjuntos foi iniciado por Georg Cantor e Richard Dedekind em 1870. Após a descoberta de paradoxos na teoria ingênua dos conjuntos, numerosos sistemas de axiomas foram propostos no início do século XX, dos quais os axiomas de Zermelo–Fraenkel, com o axioma da escolha, são os mais conhecidos.
Conceitos de teoria dos conjuntos são integrados em todo currículo de matemática nos Estados Unidos. Fatos elementares sobre conjuntos e associação de conjuntos são frequentemente ensinados na escola primária, junto com diagramas de Venn, diagramas de Euler, e as operações elementares, tais como união e interseção de conjunto. Conceitos ligeiramente mais avançados, tais como cardinalidade são uma parte padrão do currículo de matemática de graduação.
A teoria dos conjuntos é comumente empregada como um sistema precursor da matemática, particularmente na forma de teoria dos conjuntos de Zermelo–Fraenkel com o axioma da escolha. Além de seu papel fundamental, a teoria dos conjuntos é um ramo da matemática em si própria, com uma comunidade de pesquisa ativa. Pesquisas contemporâneas em teoria dos conjuntos incluem uma diversa coleção de temas, variando da estrutura do número real ao estudo da consistência de grandes cardinais.
Índice[esconder] |
[editar] História
Temas matemáticos geralmente surgem e evoluem através de interações entre muitos pesquisadores. Teoria dos conjuntos, no entanto, foi fundada por um único artigo em 1874 por Georg Cantor: "A respeito de uma propriedade característica de todos os números algébricos reais".[1][2]Desde o século V a.C., começando com o matemático grego Zenão de Eleia no ocidente e primitivos matemáticos indianos no oriente, os matemáticos têm se debatido com o conceito de infinito. Especialmente notável é o trabalho de Bernard Bolzano[3] na primeira metade do século XIX. A compreensão moderna do conceito de infinito em matemática começou em 1867–71, com os trabalhos de Cantor em teoria dos números, teoria das funções e séries trigonométricas[4]. Um encontro em 1872 entre Cantor e Richard Dedekind influenciou o pensamento de Cantor e culminou no artigo de Cantor 1874.
O trabalho de Cantor inicialmente dividiu os matemáticos de sua época. Enquanto Karl Weierstrass e Dedekind apoiavam Cantor, Leopold Kronecker, hoje visto como um dos fundadores do construtivismo matemático, era contra. A teoria dos conjuntos cantoriana, afinal, tornou-se amplamente difundida, devido à utilidade dos conceitos cantorianos, tais como correspondência um-para-um entre conjuntos, sua prova de que há mais números reais que inteiros, e a "infinidade de infinitos" ("paraíso de Cantor") que a operação conjunto das partes dá origem.
A onda de entusiasmo seguinte na teoria dos conjuntos chegou por volta de 1900, quando foi descoberto que a teoria dos conjuntos Cantoriana dava origem a várias contradições, chamadas antinomias ou paradoxos. Bertrand Russell e Ernst Zermelo encontraram o paradoxo mais simples e mais conhecido paradoxo, hoje chamado paradoxo de Russell que envolve "o conjunto de todos os conjuntos que não são membros de si mesmos". Isto leva a uma contradição, uma vez que ele deve ser e não ser um membro de si mesmo. Em 1899 Cantor se questionou: "qual é o número cardinal do conjunto de todos os conjuntos?" e obteve um paradoxo relacionado.
A força da teoria dos conjuntos foi tal que o debate sobre os paradoxos não a levou ao abandono. O trabalho de Zermelo em 1908 e Abraham Fraenkel em 1922 resultou na teoria axiomática dos conjuntos canônica ZFC, que imagina-se ser livre de paradoxos. O trabalho de analistas, como Henri Lebesgue, demonstrou a grande utilidade matemática da teoria dos conjuntos.
[editar] Conceitos básicos
Uma relação binária derivada entre dois conjuntos é a relação subconjunto, também chamada 'está contido'. Se todos os membros do conjunto A também são membros do conjunto B, então A é um subconjunto de B, denotado por A ⊆ B. Por exemplo, {1,2} é um subconjunto de {1,2,3} , mas {1,4} não é. A partir desta definição, é óbvio que um conjunto é um subconjunto de si mesmo; nos casos em que se deseja evitar isso, o termo subconjunto próprio é definido para excluir esta possibilidade.
Assim como a aritmética caracteriza operações binárias sobre números, teoria dos conjuntos caracterza operações binárias sobre conjuntos. O (A):
- União dos conjuntos A e B, denotada por A ∪ B, é o conjunto de todos os objetos que são membros de A, ou B, ou ambos. A união de {1, 2, 3} e {2, 3, 4} é o conjunto {1, 2, 3, 4}.
- Interseção dos conjuntos A e B, denotada por A ∩ B, é o conjunto de todos os objetos que são membros de ambos A e B. A interseção de {1, 2, 3} e {2, 3, 4} é o conjunto {2, 3}.
- Diferença de conjuntos de U e A, denotada por U \ A é o conjunto de todos os membros de U que não são membros de A. A diferença de conjuntos {1,2,3} \ {2,3,4} é {1}, enquanto a diferença de conjuntos {2,3,4} \ {1,2,3} é {4}. Quando A é um subconjunto de U, a diferença de conjuntos U \ A é também chamada de complemento de A em U. Neste caso, se a escolha de U é clara a partir do contexto, a notação Ac é algumas vezes usada no lugar de U \ A, particularmente se U é um conjunto universo como no estudo de diagramas de Venn.
- Diferença simétrica dos conjuntos A e B é o conjunto de todos os objetos que são membros de exatamente um de A e B (elementos que estão em um dos conjuntos, mas não em ambos). Por exemplo, para os conjuntos {1,2,3} e {2,3,4}, o conjunto diferença simétrica é {1,4}. É o conjunto diferença da união e da interseção,, (A ∪ B) \ (A ∩ B).
- Produto cartesiano de A e B, denotada por A × B, é o conjunto cujos membros são todos os possíveis pares ordenados (a,b) onde a é um membro de A e b é um membro de B.
- Conjunto das partes de um conjunto A é o conjunto cujos membros são todos os possíveis subconjuntos de A. Por exemplo, o conjunto das partes de {1, 2} é { {}, {1}, {2}, {1,2} }.
[editar] Um pouco de ontologia
[editar] Teoria axiomática dos conjuntos
Teoria elementar dos conjuntos pode ser estudada de maneira informal e intuitiva, e por isso pode ser ensinado nas escolas primárias usando, por exemplo, diagramas de Venn. A abordagem intuitiva pressupõe que um conjunto pode ser formado a partir da classe de todos os objetos que satisfaçam uma condição particular de definição. Esta hipótese dá origem a paradoxos, os mais simples e mais conhecidos dos quais são o paradoxo de Russell e o paradoxo de Burali-Forti. Teoria axiomática dos conjuntos foi originalmente concebida para livrar a teoria dos conjuntos de tais paradoxos.[5]Os sistemas mais amplamente estudados da teoria axiomática dos conjuntos implicam que todos os conjuntos formam uma hierarquia cumulativa. Tais sistemas vêm em dois sabores, aqueles cuja ontologia consiste de:
- Conjuntos sozinhos. Estes incluem a mais comum teoria axiomática dos conjuntos, teoria dos conjuntos de Zermelo–Fraenkel (ZFC), que inclui o axioma da escolha. Fragmentos de ZFC incluem:
- Teoria dos conjuntos de Zermelo, que substitui o esquema de axiomas da substituição com o da separação;
- Teoria geral dos conjuntos, um pequeno fragmento da teoria dos conjuntos de Zermelo suficiente para os axiomas de Peano e conjuntos finitos;
- Teoria dos conjuntos de Kripke-Platek, wque omite os axiomas do infinitude, conjunto das partes, e escolha, e enfraquece os esquemas de axiomas da separação e substituição.
- Conjuntos e classes próprias. Estes incluem a teoria dos conjuntos de Von Neumann-Bernays-Gödel, que tem a mesma força que ZFC para teoremas sobre conjuntos sozinhos, e teoria dos conjuntos de Morse-Kelley, que é mais forte do que ZFC.
Os sistemas de Novos Fundamentos NFU (permitindo urelementos) e NF (faltando eles) não são baseadas em uma hierarquia cumulativa. NF e NFU incluem um"conjunto de tudo", em relação a qual cada conjunto tem um complemento. Nestes sistemas urelementos importam, porque NF, mas não NFU, produz conjuntos para os quais o axioma da escolha não se verifica.
Sistemas da teoria dos conjuntos construtiva, scomo CST, CZF e IZF, firmam seus conjuntos de axiomas na lógica intuicionista em vez da lógica de primeira ordem. No entanto, outros sistemas admitem por padrão a lógica de primeira ordem , mas apresentam uma relação membro não-padrão. Estes incluem a teoria grosseira dos conjuntos e a teoria dos conjuntos difusa, na qual o valor de uma formula atômica incorporando a relação de filiação não é simplesmente Verdadeiro ou Falso. Os modelos de valores Booleanos de ZFC são um assunto relacionado.
[editar] Aplicações
Quase todos os conceitos matemáticos são agora definidos formalmente em termos de conjuntos e conceitos teóricos de conjuntos. Por exemplo, as estruturas matemáticas tão diversas como grafos, variedade, anéis, e espaços vetoriais são todos definidos como conjuntos contendo várias propriedades (axiomáticas). Equivalência e relações de ordem são onipresentes na matemática, e a teoria das relações é inteiramente baseada na teoria dos conjuntos.A teoria dos conjuntos também é um sistema fundamental para muito da matemática. Desde a publicação do primeiro volume de Principia Mathematica, que tem sido afirmado que a maioria ou mesmo todos os teoremas matemáticos podem ser derivados usando um conjunto adequadamente projetado de axiomas para a teoria dos conjuntos, aumentado com muitas definições, usando lógica de primeira ordem ou segunda ordem. Por exemplo, as propriedades do números naturais e reais podem ser obtidas da teoria dos conjuntos, já que cada sistema de números pode ser identificado como um conjunto de classes de equivalência sob uma relação de equivalência adequada cujo campo é algum conjunto infinito.
Teoria dos conjuntos como base para a análise matemática, topologia, álgebra abstrata e matemática discreta é igualmente incontroversa; matemáticos aceitam que (a princípio) teoremas nestas áreas podem ser derivadas das definições pertinentes e dos axiomas da teoria dos conjuntos. Algumas derivações completas de teoremas de complexidade matemática foram formalmente verificados a partir da teoria dos conjuntos, no entanto, tais derivações formais são muitas vezes mais extensas que do que as provas matemáticas de linguagem natural comumente presentes. Um projeto de verificação, Metamath, inclui derivações de mais de 10.000 teoremas a partir dos axiomas de ZFC e usando lógica de primeira ordem.
[editar] Áreas de estudo
Teoria dos conjuntos é a principal área de pesquisa na matemática, com muitas subáreas inter-relacionados.[editar] Teoria dos conjuntos combinatória
[editar] Teoria dos conjuntos descritiva
O campo da teoria dos conjuntos descritiva efetiva está entre a teoria dos conjuntos e a teoria da recursão. Ele inclui o estudo de lightface pointclasses, e está intimamente relacionado com a teoria hiperaritmética. Em muitos casos, os resultados da teoria dos conjuntos descritiva clássica têm versões efetivas; em alguns casos, novos resultados são obtidos provando pela versão efetiva primeiro e depois estendendo-os ("relativizando-os") para torná-la mais amplamente aplicáveis.
Uma área recente de pesquisa diz respeito a relações de equivalência de Borel e relações de equivalência decidíveis mais complicadas. Isto tem importantes aplicações para o estudo de invariantes em muitos campos da matemática.
[editar] Teoria dos conjuntos difusa
[editar] Teoria do modelo interno
O estudo de modelos de interior é comum no estudo do determinismo e grandes cardinais, especialmente quando se considera axiomas que contradizem o axioma da escolha. Mesmo que um modelo fixo da teoria dos conjuntos satisfaz o axioma da escolha, é possível que um modelo interno falhe em satisfazer o axioma da escolha. Por exemplo, a existência de cardinais suficientemente grandes implica que há um modelo interno satisfazendo o axioma do determinismo (e, portanto, não satisfazendo o axioma da escolha).[6]
[editar] Grandes cardinais
[editar] Determinismo
[editar] Forçamento
[editar] Invariantes cardinais
[editar] Topologia
[editar] Objeções à teoria dos conjuntos como fundamento para a matemática
Desde o início da teoria dos conjuntos, alguns matemáticos se opuseram a ela como um fundamento para a matemática, argumentando, por exemplo, que é apenas um jogo que inclui elementos de fantasia. A objeção mais comum à teoria dos conjuntos, um manifesto de Kronecker nos primeiros anos da teoria dos conjuntos, começou a partir da visão construtivista de que a matemática é vagamente relacionada à computação. Se este ponto de vista for admitido, então o tratamento de conjuntos infinitos, tanto na teoria ingênua dos conjuntos quanto na teoria axiomática dos conjuntos, , introduz em matemática métodos e objetos que não são computáveis. Ludwig Wittgenstein questionou a forma como a teoria dos conjuntos de Zermelo–Fraenkel manipulava infinitos. As visões de Wittgenstein sobre os fundamentos da matemática foram mais tarde criticada por Georg Kreisel e Paul Bernays, e minuciosamente investigadas por Crispin Wright, entre outros.Teóricos das categorias propuseram a teoria de topos como uma alternativa à tradicional teoria axiomática dos conjuntos. Teoria de topos pode interpretar várias alternativas para aquela teoria, tais como o construtivismo, a teoria dos conjuntos finitos, e a teoria dos conjuntos computáveis.[carece de fontes]
[editar] Ver também
[editar] Referências
- ↑ G. Cantor, Über eine Eigenschaft des Inbegriffes aller reellen algebraischen Zahlen, Crelles Journal f. Mathematik, 77 (1874) 258–262.
- ↑ Philip Johnson, 1972, A History of Set Theory, Prindle, Weber & Schmidt ISBN 0871501546
- ↑ Bernard Bolzano, Paradoxien des Unendlichen, 1920, Felix Meiner, Leipzip.
- ↑ Georg Cantor, 1932, Gesammelte Abhandlungen mathematischen und philosophischen Inhalts, Springer, Berlin.
- ↑ Em seu artigo de 1925, John von Neumann observou que "a teoria dos conjuntos na sua versão primeira, "ingênua", devida a Cantor, levou a contradições. Essas são as bem conhecidas antinomias do conjunto de todos os conjuntos que não contêm a si próprios (Russell), do conjunto de todos os números ordinais transfinitos (Burali-Forti), e o conjunto de todos os números reais finitamente definíveis (Richard)." Ele vai adiante até observar que duas "tendências" estavam tentando "reabilitar" a teoria dos conjuntos. Sobre o primeiro esforço, exemplificado por Bertrand Russell, Julius König, Hermann Weyl e L. E. J. Brouwer, von Neumann disse que "o efeito geral de suas atividadas. . . devastador". Com relação ao método axiomático empregado pelo segundo grupo composto de Zermelo, Abraham Fraenkel e Arthur Moritz Schoenflies, von Neumann demonstrou preocupação de que "vemos apenas que os modos conhecidos de inferência que levam a antinomias falham, mas quem sabe onde não há outras?" e ele assumiu a tarefa de, "no espírito do segundo grupo, produzir, por meio de um número finito de operações puramente formais . . . todos os conjuntos que desejamos ver formados" mas não permitir as antinomias. (Todas as citações de von Neumann 1925 reimpresso em van Heijenoort, Jean (1967, third printing 1976), "From Frege to Gödel: A Source Book in Mathematical Logic, 1979-1931", Harvard University Press, Cambridge MA, ISBN 0-674-32449-8 (pbk). Uma sinopse da história, escrita por van Heijenoort, pode ser encontrada nos comentários que precedem o artigo de von Neumann de 1925.
- ↑ Jech, Thomas (2003), Set Theory: Third Millennium Edition, Springer Monographs in Mathematics, Berlin, New York: Springer-Verlag, ISBN 978-3-540-44085-7 , p. 642.
[editar] Leituras adicionais
- Keith Devlin, (2nd ed.) 1993. The Joy of Sets. Springer Verlag, ISBN 0-387-94094-4
- Ferreirós, Jose, 2007 (1999). Labyrinth of Thought: A history of set theory and its role in modern mathematics. Basel, Birkhäuser. ISBN 978-3-7643-8349-7
- Johnson, Philip, 1972. A History of Set Theory. Prindle, Weber & Schmidt ISBN 0871501546
- Kunen, Kenneth, Set Theory: An Introduction to Independence Proofs. North-Holland, 1980. ISBN 0-444-85401-0.
- Tiles, Mary, 2004 (1989). The Philosophy of Set Theory: An Historical Introduction to Cantor's Paradise. Dover Publications.
[editar] Ligações externas
Multiconjunto
Origem: Wikipédia, a enciclopédia livre.
Matematicamente, um multiconjunto é a generalização de um conjunto, de tal forma que permite a repetição de elementos.Por exemplo, M = {a, b, c, c, d, e, e} é um multiconjunto distinto de X = {a, b, c, d, e}, mas se M e X fossem conjuntos, teríamos M=X.
Índice[esconder] |
[editar] Definição formal
Um multiconjunto é definido como um par (A,m), onde A é um conjunto qualquer, e a função que associa a cada elemento de A um número natural, onde consideramos a definição de números naturais que não contêm o zero, ou seja
a função que associa a cada elemento de A um número natural, onde consideramos a definição de números naturais que não contêm o zero, ou seja 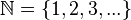 .
.A multiplicidade de um elemento a é definido como m(a).
Representamos um multiconjunto com a mesma notação que usamos para conjuntos, mas citamos m(i) vezes um elemento i do multiconjunto.
Por exemplo, o multiconjunto M com o par (A, m), tal que A = {a,b,c,d,e} e m(a)=1, m(b)=1, m(c)=2, m(d)=1, m(e)=2, é representado por M = {a,b,c,c,d,e,e}. A ordem dos elementos, assim como nos conjuntos, não importa.
Como os multiconjuntos são uma generalização de conjuntos, um multiconjunto B é um conjunto quando m(i) = 1 para todo
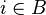 .
.[editar] Exemplos
Multiconjuntos aparecem naturalmente em vários contextos:- Na fatoração: a forma natural de se expressar a fatoração de um número natural ou um polinômio é através de multiconjuntos. Por exemplo, os fatores primos de 12 são {2, 2, 3}, e os fatores primos de 18 são {2, 3, 3}.
- A solução de uma equação polinomial é um multiconjunto, já que é importante indicar a multiplicidade de cada raiz.
[editar] Cardinalidade de um multiconjunto
A cardinalidade de um multiconjunto M = (A,m) é definida como: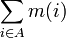 .
.[editar] Seleção com repetição
Em análise combinatória, multiconjunto é uma seleção com repetição. Em uma seleção em combinatória, a ordem não é importante.Para calcular o número de multiconjuntos com k elementos escolhendo entre n tipos de elementos.
- Exemplos
É só selecionar dois dos 8 números possíveis. Neste caso os espaços nos dominós são iguais.
Podemos considerar a seqüência seguinte:
- X4 + X3 + X2 + X1 = 18, Xi = número de bolas da i-ésima caixa
Hiperconjunto
Origem: Wikipédia, a enciclopédia livre.
Em ZFC sem o axioma da regularidade, a possibilidade de infundados conjuntos surgem. Estes conjuntos, se existem, são também chamados hiperconjuntos. Claramente, se A ∈ A, então A é um hiperconjunto.Em 1988, Peter Aczel publicou um trabalho influente, Non-Well-Founded Sets (Conjuntos Não-Bem-Fundados). A teoria dos hiperconjuntos tem sido aplicada à ciência computacional (processamento algébrico e semântica limite), linguística (teoria da situação), e filosofia (trabalho sobre o paradoxo de Liar).
[editar] Tipos
Três distinctos anti-fundamentos axiomáticos são bem conhecidos:- AFA ("Axioma do Anti-Fundamento") — atribuído a M. Forti e F. Honsell, e também conhecido como axiona anti-fundação de Aczel;
- FAFA ("AFA de Finsler") — atribuído a P. Finsler;
- SAFA ("AFA de Scott") — atribuído a Dana Scott.
Função
Origem: Wikipédia, a enciclopédia livre.
(Redirecionado de Funções)
-
 Nota: Para outros significados, veja Função (desambiguação).
Nota: Para outros significados, veja Função (desambiguação).
Índice[esconder] |
[editar] Conceito
As funções são definidas abstractamente por certas relações. Por causa de sua generalização as funções aparecem em muitos contextos matemáticos e muitas áreas desta ciência baseiam-se no estudo de funções. Pode notar-se que as palavras: função; mapeamento; mapear; e transformar são geralmente usadas como termos equivalentes. Além disso funções podem ocasionalmente ser referidas como funções bem definidas ou função total. O conceito de uma função é uma generalização da noção comum de fórmula matemática. As funções descrevem relações matemáticas especiais entre dois elementos. Intuitivamente, uma função é uma maneira de associar a cada valor do argumento x um único valor da função f(x). Isto pode ser feito especificando através de: uma equação, um relacionamento gráfico; diagramas representando os dois conjuntos; uma regra de associação; uma tabela de correspondência. Cada par de elementos relacionados pela função determina um ponto nesta representação, a restrição de unicidade da imagem implica um único ponto da função em cada linha de chamada do valor independente x. [3][4].A noção intuitiva de funções não se limita a computações usando apenas números. A noção matemática de funções é bem mais ampla. Assim, uma função liga um domínio (conjunto de valores de entrada) com um segundo conjunto o contradomínio ou codomínio (conjunto de valores de saída) de tal forma que a cada elemento do domínio está associado exatamente um elemento do contradomínio. O conjunto dos elementos do contradomínio que são relacionados pela f a algum x do domínio, é o conjunto imagem ou chamado simplesmente imagem.[4]
[editar] Definição formal
Considere dois conjuntos: o conjunto X com elementos x e o conjunto Y com elementos y. Isto é:Outra maneira de dizer isto é afirmar que f é uma relação binária entre os dois conjuntos tal que:
- f é unívoca: se y = f (x) e z = f (x), então y = z;
- f é total: para todos x em X, existe um y em Y tal que y = f (x).
Se a primeira condição é atendida, mas a segunda não, temos uma função parcial.
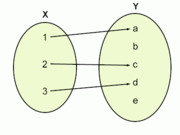
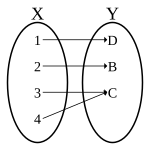
Considere as três funções seguintes:
 | Esta não é uma função, pois o elemento 3 em X é associado com dois elementos (d e c) em Y (a correspondência é funcional). Apesar de não ser uma função, representa uma função multivalorada. |
 | Esta não é uma função, pois o elemento 1 em X não é associado com um elemento em Y. Apesar de não ser uma função, representa uma função parcial. |
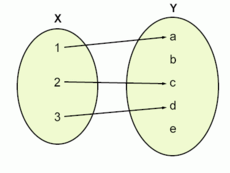 | Esta é uma função (no caso, uma função discreta). Ela pode ser definida explicitamente pela expressão: |
[editar] Elementos da função

Função x2, definida para { -3,-2,-1,0 }. Observar o conjunto domínio (D), contradomínio (CD) e imagem (delineado pela linha tracejada).
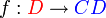 uma função. Toda função consta de três partes:
uma função. Toda função consta de três partes:- A primeira é o conjunto
 , chamado de domínio da função, é o conjunto onde a função é definida [5], ou seja, ele contém todos os elementos x para os quais a função deve ser definida.
, chamado de domínio da função, é o conjunto onde a função é definida [5], ou seja, ele contém todos os elementos x para os quais a função deve ser definida. - Outra parte integrante da função é o contradomínio (representado na figura por
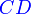 ), que é o conjunto que contém os elementos que podem ser relacionados a elementos do domínio. Em outras palavras, é o conjunto onde a função toma valores.[5] Dentro do contradomínio, define-se o conjunto imagem como o conjunto de valores que efetivamente f(x) assume. O conjunto imagem é, pois, sempre um subconjunto do contradomínio.
), que é o conjunto que contém os elementos que podem ser relacionados a elementos do domínio. Em outras palavras, é o conjunto onde a função toma valores.[5] Dentro do contradomínio, define-se o conjunto imagem como o conjunto de valores que efetivamente f(x) assume. O conjunto imagem é, pois, sempre um subconjunto do contradomínio. - A terceira parte de uma função é a regra que permite associar, de modo bem determinado, a cada elemento
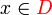 , um único elemento
, um único elemento 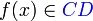 , chamado o valor que a função assume em x (ou no ponto x).[5]
, chamado o valor que a função assume em x (ou no ponto x).[5]
 é diferente da função
é diferente da função  , pois o contradomínio é diferente.
, pois o contradomínio é diferente.[editar] Gráficos de função
Uma função é determinada pelo seu gráfico e pela especificação do conjunto de chegada. Assim, se duas funções têm o mesmo gráfico, uma poderá ser sobrejectiva e a outra não. No entanto, a injectividade de uma função é completamente determinada pelo gráfico.
[editar] Classificação das funções
[editar] Quanto ao número de elementos na imagem
Os tipos de funções podem ser classificados de acordo com o seu comportamento com relação à regra uma única saída para cada entrada. Como não foi dito nada sobre as entradas, ou se as saídas tem que ser únicas temos que resolver estas ambiguidades. Ao fazer isto encontramos apenas três tipos de classes de funções, e classe é empregado aqui como classificação mesmo e não como classe de equivalência. [6]| Tipo de função | Característica da função | Conjunto imagem | Explicação visual | Exemplo | Admite função inversa? É inversível? |
|---|---|---|---|---|---|
| Função injetora ou injetiva | Cada elemento da imagem está associado a apenas um elemento do domínio, isto é, quando x ≠ y no domínio e f(x) ≠ f(y) no contradomínio. A cardinalidade do contradomínio é sempre maior ou igual à do domínio. | O número de elementos no contradomínio pode ser igual ou maior que na imagem da função. | A função f: N 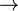 N dada por f(x) = 2x, é injetiva porque, sempre que toma-se dois valores diferentes de x: a ≠ b, obtém-se valores diferentes para f(x): f(a) ≠ f(b). N dada por f(x) = 2x, é injetiva porque, sempre que toma-se dois valores diferentes de x: a ≠ b, obtém-se valores diferentes para f(x): f(a) ≠ f(b). | Não sempre, mas sempre admite inversa à esquerda. | |
| Função sobrejetora ou sobrejetiva | Todos os elementos do contradomínio estão associados a algum elemento do domínio. | O conjunto imagem é igual ao conjunto contradomínio | A função f: R 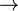 R dada por f(x) = 6x, não é sobrejetiva, pois o número -1 é elemento do contradomínio R e não é imagem de qualquer elemento do domínio. R dada por f(x) = 6x, não é sobrejetiva, pois o número -1 é elemento do contradomínio R e não é imagem de qualquer elemento do domínio. | Não sempre, mas sempre admite inversa à direita. | |
| Função bijetora ou bijetiva | São ao mesmo tempo sobrejetoras e injetoras, isto é, todos os elementos do domínio estão associados a todos os elementos do contradomínio de forma um para um e exclusiva. | O conjunto imagem é igual ao conjunto contradomínio | A função f: N 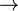 N dada por f(x) = x, é bijetiva porque é sobrejetiva e injetiva ao mesmo tempo. Exemplo: função identidade N dada por f(x) = x, é bijetiva porque é sobrejetiva e injetiva ao mesmo tempo. Exemplo: função identidade | Sim, sempre; imagem igual ao contradomínio vira domínio e vice-versa. |
[editar] Quanto ao tipo de regra
Uma função pode ser classificada de acordo com o tipo de regra que associa os elementos do domínio aos elementos do contradomínio.[6] Se a regra que associa o domínio ao contradomínio é um polinômio, então a função é dita uma Função polinomial. Exemplos de funções polinomiais são a função linear e a função quadrática.[6] Se a regra eleva o logaritmo neperiano pelos elementos do domínio, então a função é dita exponencial.[6][editar] Quanto à convexidade
[editar] Funções implícitas e explicitas
O tipo de função mais comum é aquele onde o argumento e o valor da função são ambos numéricos, o relacionamento entre os dois é expresso por uma fórmula e o valor da função é obtido através da substituição direta dos argumentos. Considere o exemplo:[editar] Funções compostas
São as funções em que o conjunto imagem de uma função f(x) serve de domínio para uma outra função g(x), que por sua vez gera um conjunto imagem A. A função composta é uma expressão que, dado um determinado número do domínio de f(x), nos leva diretamente ao conjunto imagem A. Por exemplo, dadas as funções:- f(x) = 2x + 3 e g(x) = x − 1
- g(f(x)) = 2x + 2
[editar] História
Como um termo matemático, função foi introduzido por Gottfried Leibniz em 1694, para designar qualquer das várias variáveis geométricas associadas com uma dada curva; tais como a inclinação da curva ou um ponto específico da dita curva. Funções relacionadas às curvas são atualmente chamadas funções diferenciáveis e são ainda o tipo de funções mais encontrado por não-matemáticos. Para este tipo de funções, pode-se falar em limites e derivadas; ambos sendo medida da mudança nos valores de saída associados à variação dos valores de entrada, formando a base do cálculo infinitesimal.A palavra função foi, posteriormente, usada por Euler em meados do século XVIII para descrever uma expressão envolvendo vários argumentos. Com o tempo foi-se ampliando a definição de funções. Os matemáticos foram capazes de estudar "estranhos" objetos matemáticos tais como funções que não são diferenciáveis em qualquer de seus pontos. Tais funções, inicialmente tidas como puramente imaginárias e chamadas genericamente de "monstros", foram já no final do século XX, identificadas como importantes para a construção de modelos físicos de fenômenos tais como o movimento Browniano.
Durante o Século XIX, os matemáticos começaram a formalizar todos os diferentes ramos da matemática. Weierstrass defendia que se construisse o cálculo infinitesimal sobre a Aritmética ao invés de sobre a Geometria, o que favorecia a definição de Euler em relação à de Leibniz. Mais para o final do século, os matemáticos começaram a tentar formalizar toda a Matemática usando Teoria dos conjuntos, e eles conseguiram obter definições de todos os objetos matemáticos em termos do conceito de conjunto. Foi Dirichlet quem criou a definição "formal" de função moderna. Na definição de Dirichlet, uma função é um caso especial de uma relação. Relação é um conjunto de pares ordenados, onde cada elemento do par pertence a um dos conjuntos relacionados. Nas relações não existem restrições quanto à lei de correspondência entre os elementos dos conjuntos, já para as funções é costume introduzir restrições. Na maioria dos casos de interesse prático, entretanto, as diferenças entre as definições moderna e de Euler são desprezáveis.
Referências
- ↑ STEWART, James. Cálculo Vol. I - 4ª edição. São Paulo: Pioneira Thomson Learning, 2002. Página 12.
- ↑ FRANK AYRES, Philip A. Schmidt. Matemática para Ensino Superior - 3ª edição. São Paulo: Editora Artmed, 2003. Página 16.
- ↑ a b STEWART, James. Cálculo Vol. I - 4ª edição. São Paulo: Pioneira Thomson Learning, 2002.
- ↑ a b FRANK AYRES, Philip A. Schmidt. Matemática para Ensino Superior - 3ª edição. São Paulo: Editora Artmed, 2003.
- ↑ a b c LIMA, Elon Lages. Curso de análise volume 1. 11ª edição, 2004. página 13
- ↑ a b c d e AUBYN, António St.; FIGUEREDO, Maria C.; LAURA, Luís de; RIBEIRO, Luisa; VIEGAS, Francisco. Funções.Lisboa, 2004.Dísponível